how to find the surface area of a trapezoidal prism

What is a trapezoid? A trapezoid or trapezium is a quadrilateral with at to the lowest degree one pair of parallel sides. The parallel sides are known as bases. When the other ii sides are non-parallel, they are chosen legs or lateral sides. Else there are 2 pairs of bases. Real-life examples where you can see the surface area of trapezoids are handbags, popcorn tins, and the guitar-like dulcimer. The surface area of a trapezoid is the complete infinite enclosed past its 4 sides. There are 2 approaches to finding the expanse of trapezoids.

The first method is a direct method that uses a direct formula to find the area of a trapezoid with the known dimensions (see example 1)
For the 2nd method, firstly, if we are given the length of all the sides, we split the trapezoid into smaller polygons such as triangles and rectangles. Next, we will find the area of the triangles and rectangles separately. Finally, nosotros will add the area of the polygons to get the total expanse of the trapezoid. (run into case 2 for a more than precise understanding)

What is the Formula To Calculate the Area of Trapezoids?

We can summate the area of a trapezoid if nosotros know the length of its parallel sides and the altitude (top) between the parallel sides. The area of trapezoids formula is:

A = ½ (a + b) h

Hither (A) is the area of a trapezoid.

'a' and 'b' are the parallel sides of trapezoid

'h' is the peak, i.e., the perpendicular distance between the parallel sides.

Area of Trapezoid Example

Here is an area of a trapezoid case using the direct formula and an area of a trapezoid example with the alternative method.

Example 1: Find the area of a trapezoid given the length of parallel sides 22 cm and 12 cm, respectively. The height is v cm.

Solution: Given: The bases are : a = 22 cm; b = 10 cm; the elevation is h = 5 cm.
The area of the trapezoid = A = ½ (a + b) h
A = ½ (22 + 10) × (5)
A = ½ (32) × (five)
A = ½ × 160
A = lxxx cmⁱⁱ

Example 2: Find the surface area of a trapezoid whose parallel sides are given equally 10cm and 16cm, respectively, and the non-parallel sides are 5cm each.

Solution: Since in this question, nosotros don't accept the height of the trapezium, we will follow the following steps to calculate the area of the trapezoid.
Given: a =10 cm; b =16 cm; non-parallel sides = v cm each

Footstep 1: To find the height of the trapezoid, we will get-go draw the height of the trapezoid on both sides. Now nosotros tin see that the trapezoid consists of a rectangle ABQP and 2 correct-angled triangles, APD and BQC.

Step 2: Now, we take to find the length of DP and QC.
Since ABQP is a rectangle, AB = PQ
DC = 16 cm (Given)
Then, PQ = AB
We tin can notice the combined length of DP + QC every bit follows
DC – PQ = 16 – 10 = 6 cmSo, DP + QC = 6
six ÷ 2 = DP = QC
three cm = DP = QC

Step 3: AP = BQ (contrary and equal sides of a rectangle)
Advertisement = BC = 5 cm
(Given) So, we tin calculate the elevation AP and BQ using Pythagoras theorem.
In the right-angled triangle ADP
AP = √(Ad² – DPⁱⁱ)
AP = √(five² – 3²)
AP = √(25 – ix) = √16 = iv cm
Since ABQP is a rectangle, the contrary sides volition exist equal. So, AP = BQ = 4 cm.

Footstep iv: Now nosotros know all the dimensions of the trapezoid. We tin can summate the area using the formula.
Area of a trapezoid = ½ (a + b) h; where h = iv cm, a =10 cm b = 16 cm
On substituting values we get:
Area = ½ (ten + 16) × 4
Expanse = ½ × 26 × 4
Area = 52 cm²

We can calculate by adding area of the rectangle and two triangles
Expanse of trapezoid = Expanse of ABPQ + Area of ADP + Expanse of BQC
Expanse of trapezoid = (l × b) + 2( ab/two)
Area of trapezoid = (ten × 4) + 2(three ×4/2)
A = xl + 12
A = 52 cmⁱⁱ

Trapezoidal Prism

A trapezoidal prism is a 3D effigy made up of two coinciding trapezoids that are connected by four rectangles. The trapezoids are on the top and the bottom. Thus, they form the base of operations for prisms have polygons that form their bases. The four rectangles form the lateral faces of the trapezoid prism. So, a trapezoidal prism consists of-

Six faces
Eight vertices
Twelve edges

Surface Surface area of a Trapezoidal Prism

Area of a trapezoidal prism is the sum of the surfaces of the prism. This surface area equals the areas of all of the faces of the trapezoid prism. Since a trapezoidal prism has ii trapezoidal faces and four rectangular faces, a sum of their areas will give the surface area of the prism. Withal, there is a simple and direct formula for calculating the surface expanse of a trapezoid prism. The formula is:

Surface Expanse of a Trapezoidal Prism = h (b + d) + l (a + b + c + d) unit foursquare.

Here, h = height

b and d are the lengths of the base

a + b + c + d is the perimeter

fifty is the lateral surface area of a trapezoidal prism

Derivation of Surface Expanse of a Trapezoidal Prism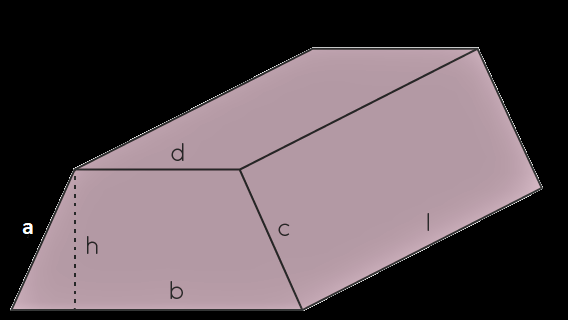

The base of a trapezoidal prism is trapezoid in shape. Here,

b and d are parallel sides of the trapezoid

H = distance between the parallel sides

l = length of the trapezoidal prism

So, the total surface area of a trapezoidal prism (TSA) = 2 × areas of base + lateral surface area ————- (1)

Area of a trapezoid = ½ (base ane + base of operations 2) summit

So, area of trapezoidal base of operations = h (b + d)/2 ——————— (two)

The lateral surface area of a trapezoidal prism (LSA) = sum of the areas of each rectangular surface

So, LSA = (a × l) + (b × l) + (c × l) + (d × l) ——————- (three)

On substituting the values from equation (2) and equation (three) in equation 1 i.eastward., TSA formula, nosotros get:

(TSA) = two × h (b + d)/two + (a × l) + (b × 50) + (c × l) + (d × 50)

TSA = h (b + d) + [(a × l) + (b × fifty) + (c × l) + (d × l)]

Total surface surface area of a trapezoidal prism = h (b + d) + 50 (a + b + c + d)

Thus, TSA of a trapezoidal prism = h (b + d) + l ( a + b + c + d) unit square

How to Find the Surface Area of a Trapezoidal Prism?

Here are the steps on how to find the surface area of a trapezoidal prism.

Step 1: Spot the iv sides of the trapezium – a, b, c, and d. These correspond the widths of the 4 rectangles. The addition of these 4 values will requite the perimeter P.

Step 2: Spot the length h of the prism.

Stride 3: Find the lateral surface area of a trapezoidal prism.

Stride 4: Identify b1, b2 and h of the trapezoid. Now, find the base area B using the formula, (b1 + b2) h/2

Footstep 5: Lastly, put the values in the formula = 2B + Lateral Area to summate the total surface surface area of the trapezoidal prism.

Consider the following example of the expanse of a trapezoidal prism for a clearer understanding.

Instance i: Find the full surface area of an isosceles trapezoidal prism that has parallel edges of the base viii cm and 12 cm. The legs of the base of operations are 5 cm each, the altitude of the base is 4 cm and the height of the prism is 10 cm.

Solution: The perimeter of the base = sum of the length of the sides.
p=viii+5+12+five=30 cm
Given that the base is an isosceles trapezoid, therefore, the expanse = one/2h(b1+b2)
Surface area of base =one/2(4)(viii+12)=40 cm²
T.S.A.= ph+2B
T.South.A = 30(10)+ii(40)
T.Southward.A =300+fourscore =380 cmⁱⁱ

Source: https://www.turito.com/learn/math/area-of-trapezoid

Posted by: faydoely1954.blogspot.com